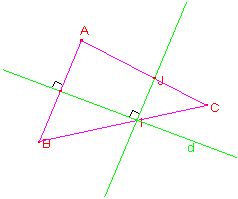
Dans la figure ci dessus le codage montre que (IJ) est perpendiculaire à (d) et que (AB) est aussi perpendiculaire à (d)
Comme (IJ) et (AB) sont perpendiculaires à (d)
Alors elles sont parallèles entre elles.
Donc (AB) est parallèleà (IJ)
La démonstration en géométrie en 4ème
0)Pourquoi démontrer ?
En géométrie on démontre en général, pour vérifier que ce qu'on voit sur une figure est vrai.
Donc avant de faire une démonstration, il faut récolter toutes les informations que nous donne l'énoncé et faire la différence entre ce qui est donné et ce que l'on croit voir.
Exemple : Donc si deux droites ont l'air d'être parallèles et que dans l'énoncé, il n'est pas indiqué que les droites sont parallèles on ne peut pas supposer que ces droites sont parallèles. Il faudra alors le prouver avant d'utiliser cette propriété.
I) Comment démontrer que deux droites sont parallèles
6ème
Méthode 1:
Si deux droites sont perpendiculaires à
une même droite
Alors elles sont parallèles entre
elles
Exemple :
On donne la figure suivante montrer que (AB) est parallèle à
(IJ)

Dans
la figure ci dessus le codage montre que (IJ) est perpendiculaire à
(d) et que (AB) est aussi perpendiculaire à (d)
Comme (IJ) et (AB) sont perpendiculaires à (d)
Alors elles sont parallèles entre elles.
Donc (AB) est parallèleà (IJ)
5ème
Méthode 2 :
Si deux angles alternes internes sont égaux
Alors les droites qui les forment sont
parallèles
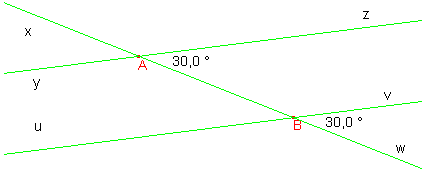
Exemple montrer que les droites (yz) et (uw) sont parallèles

Dans la figure ci dessus les angles
![]() et
et
![]() sont alternes internes et égaux formés par les droites
(yz) et (uw) et la sécante (AE) donc les droites (yz) et (uw)
sont parallèles
sont alternes internes et égaux formés par les droites
(yz) et (uw) et la sécante (AE) donc les droites (yz) et (uw)
sont parallèles
Méthode 3 :
Si deux angles correspondants sont égaux
Alors les droites qui les forment sont
parallèles
Exemple
Dans
la figure ci dessus les angles
![]() et
et
![]() sont correspondants et égaux formés par les droites
(yz) et (uw) et la sécante (AE) donc les droites (yz) et (uw)
sont parallèles
sont correspondants et égaux formés par les droites
(yz) et (uw) et la sécante (AE) donc les droites (yz) et (uw)
sont parallèles
Méthode 4 :
Si deux droites sont formées par
les côtés opposés d'un parallélogramme
Alors ces droites sont parallèles
4ème
Méthode 5 :
Premier théorème des
milieux
Dans un triangle si une droite passe
par le milieu de deux côtés
Alors elle est parallèles au
troisième côté
II) Comment montrer qu'un point est le milieu d'un segment
6ème
Méthode 1 :
Si un point appartient à un
segment et à sa médiatrice
Alors il est au milieu de ce segment
5ème
Méthode 2 :
Si A est le symétrique de B par
rapport à O
Alors O est le milieu de [AB]
Méthode 3 :
Dans un parallèlogramme les
diagonales se coupent en leur milieu
4ème
Méthode 4 :
Dans un triangle, Si une droite passe
par le milieu d'un côté et est parallèle à
un deuxième côté
Alors elle passe par le milieu du
troisième côté.
Méthode 5:
Dans le triangle ABC , la médiane
issue de A, passe par le milieu de [BC]
III) Comment montrer que deux droites sont perpendiculaires.
6ème
Méthode 1
La médiatrice d'un segment est
la droite perpendiculaire à ce segment passant par son milieu
Méthode 2
Si deux droites sont parallèles entre elles si une droite est perpendiculaire à l'une d'elles
alors elle est perpendiculaire à l'autre
5ème
Méthode 3
Deux droites qui forment entre elles un
angle de 90° sont perpendiculaires entre elles
4ème
Methode 4
Dans le triangle ABC
la hauteur issue de A est
perpendiculaire à [BC]
IV) Comment montrer une égalité de quotient ou calculer un quotient
4ème
En général il faut penser à la propriété de Thalès