Pour représenter la fraction
d’un
objet on divise cet objet en b parties égales et on en prend a
parties.LES FRACTIONS
1)Représentation
de la fraction d’un objet
Pour représenter la
fraction
d’un
objet on divise cet objet en b parties égales et on en prend a
parties.
Exemple :
Représenter
de
ce carré
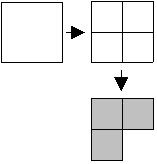
On commence par diviser ce carré en 4 parties égales et on en prend 3
Représenter
de
ce carré
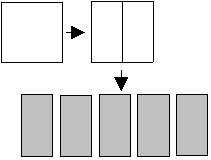
On commence par diviser ce carré en 2 parties égales et on en prend 5
b) Fraction et nombre
Une
fraction représente aussi un nombre. La fraction
est égale à
Définition : (Droite graduée)
Une droite graduée est une droite sur laquelle on a fixé une origine et une unité de mesure
Définition : (Abscisse d'un point)
Un point est repéré sur une droite graduée par un nombre appelé abscisse de ce point , c'est la distance entre l'origine est ce point.
c)
Fraction d’une quantité
Pour calculer
les
d’une quantité, on multiplie cette quantité par
.
Règle
Si a, b et c sont trois nombres avec c
,
Alors
a)Egalité
de deux fractions
Deux fractions sont égales si le
numérateur et le dénominateur de l’une sont
obtenu en multipliant (ou en divisant) le numérateur et le
dénominateur de l’autre par un même nombre
différent de zéro.
Règle :
Si a, b et k sont trois nombres avec k différent de zéro
Alors
on a aussi
Exemple :
ou
b)Simplification
d'une fraction
Simplifier une fraction c'est trouver une
fraction égale dont le numérateur et le dénominateur
sont plus petit que la première fraction.
Si une fraction
ne peut pas être simplifier on dit qu'elle est irréductible
Exemple
Simplifier
on
sait que
donc
Rappel des règles de divisibilité par 2, 3, 5 et 10
Par
2 :Un nombre entier est
divisible par 2 lorsqu'il se termine par 0, 2, 4, 6 ou 8
Exemple
544 est divisible par 2 car il se termine par 4
par
3 : Un nombre entier est
divisible par 3 lorsque la somme de ses chiffres est dans la table
de 3
Exemple 252 est divisible par 3 car
2+5+2=9 et 9 est dans la table de 3
Par 5 : Un nombre entier est divisible par 5 lorsqu'il
se termine par 0 ou 5.
Exemple 545 et 230 sont
divisible par 5.
Par 9: Un nombre entier est divisible par 9 lorsque la somme de ses chiffres est dans la table de 9
Exemple 8271 est divisible par 3 car 8+2+7+1=18 et 18 est dans la table de 9.
Par 10 : Un nombre entier est divisible par 10
lorsqu'il se termine par 0.
Exemple 5210 sont
divisible par 10.
c)
Comparaison de deux fractions
c1) les deux fractions ont le même
numérateur
La fraction la plus grande est celle
qui a le plus petit numérateur
Exemple
est
plus grand que
c2)
Si les deux fractions ont le même dénominateur
La
fraction la plus grande est celle qui a le plus grand
numérateur
Exemple
est
plus grand que
c3)
Si les deux fractions n'ont pas le même dénominateur
On
met les deux fractions au même dénominateur et on
applique la règle précédente
Exemple
Comparer
et
Comme 5 est plus petit que 9
donc
on a
alors
III) Addition et soustraction de fractions
Les deux fractions ont le même dénominateur
On additionne (ou on soustrait) les numérateurs entre eux et on garde le dénominateur commun
Si a, b et c sont trois nombres avec c différent de zéro
Alors
on a aussi
1)
2)
Les deux fractions ont un dénominateur différent
On ramène les deux fractions aux même dénominateur et on applique la règle ci-dessus.
2)
On
regarde les tables de 4 et 6
On a 6x1=6 ; 6x2=12 et
3x4=12
On peut prendre 12 comme dénominateur commun
et
donc
Pour multiplier deux fractions on multiplie les numérateurs entre eux et les dénominateurs entre eux.
Règle :
Si a, b, c et d sont quatre nombres avec b
et d différent de zéro Alors
Remarque : Dans un produit de deux fractions on ne ramène pas les fractions au même dénominateur.