Chapitre 11 : Pyramides et cônes
Les pyramides
Définition : Une pyramide est un solide dont :
Une face (sa base) est un polygone qui ne contient pas le sommet S
Les faces latérales qui sont des triangles qui ont pour sommet S
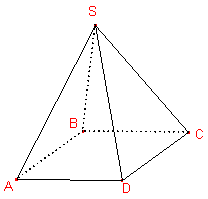
Exemple : SABCD est une pyramide de sommet S

Définition : La hauteur d'une pyramide est le segment [SH] où H est un point de la base et [SH] est perpendiculaire à la base.
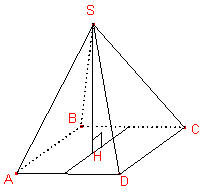
Pyramides régulières :
C'est une pyramide dont la base est formée par un polygone régulier (triangle rectangle, carré,...)
Propriété : Si une pyramide est une pyramide régulière
Alors ses faces latérales sont des triangles isocèles superposables.
Volume d'une pyramide
Le volume d'une pyramide est donné par la formule
![]()
II ) Cône de révolution
Un cône de révolution est un solide engendré par la rotation d'un triangle rectangle autour d'un de ses côtés.
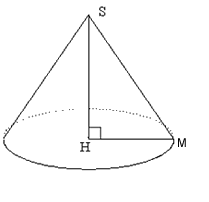
Volume
d'un cône de révolution :
![]()
Patron d'un cône
Construire le patron d'un cône dont la surface de base à un rayon de 3 cm et de 4 cm de hauteur
 Ici
SH=4 cm, On calcule SM
Ici
SH=4 cm, On calcule SM
Le triangle SHM est rectangle en H, d'après
le théorème de
Pythagore
SM²=SH²+MH²
SM²=3²+4²=9+16=25
SM=5
Le périmètre du disque de
base est
![]()
La longueur du grand cercle est égale
à
![]()
Il faut trouver la valeur de l'angle ISJ
La longueur de l'arc l'arc